CS35: Final Exam Study Guide

In addition to all concepts from Quiz 1, Quiz 2, and Quiz 3,

You should be able to define or explain the following terms:

• The Dictionary abstract data type
• Hash tables, hash functions, hash code, a hash table's load factor
• Importance of hash functions, load factors, capacity, etc in performance
• Separate Chaining and Linear Probing (as well as possible extensions)
• Tradeoffs between BST and HashTable dictionary representations
• Various strategies for handling keys (e.g., allowing duplicates in priority queues vs unique keys in BST and Dictionaries)
• graph, vertex, edge
• directed, undirected graphs
• weighted, unweighted graphs
• adjacent, neighbor, outgoing edges, incoming edges, out-degree, in-degree, degree
• path, reachable, path length, distance, cost
• adjacency-list representation, adjacency-matrix representation
• breadth-first search, depth-first search of a graph
• shortest path problem
• Dijkstra's algorithm
• Topological Sort (superficial knowledge)
• trees (superficial knowledge)
• spanning tree, minimum spanning tree (MST) (superficial knowledge)
• Prim's algorithm for discovering an MST (superficial knowledge)

You should be familiar with the following C++-related concepts:

• testing strategies (cout statements, unit tests, gdb, valgrind)
• STL classes, including vector and pair
• Expanding capacity in a hash table (or ArrayList, or BinaryHeap)
• throwing exceptions and try/catch blocks

Practice problems

1. Using the LinkedBST representation you saw in class, describe the sequence of recursive calls made by the fourth insert function in the code below.

   int main() {
   BST<int, string> *dict = new LinkedBST<int, string>();
     dict->insert(5, "puppies");
     dict->insert(9, "kittens");
     dict->insert(11, "foals");
   
     // trace through the following function
     dict->insert(10, "calves");
   
     cout << "goodbye!" << endl;
   }
   

2. Using separate chaining to resolve hash collisions, insert the following five items into a hash table of capacity 5, in the order given (from top to bottom):

   Key	Hash value
   A	1
   B	1
   C	1
   D	0
   E	2



3. Repeat using linear probing to resolve hash collisions, instead of chaining.


4. Successively remove the keys A, B then C from the hash table that used linear probing in the previous question.


5. Consider the following hash function, like the function in hashTable-inl.h:

     int hash(int key, int capacity) {
       return key % capacity;
     }
   

   1. Suppose we have an empty hash table with capacity C. Complete the following code so that the total running time is asymptotically proportional to C^2:

        HashTable<int,string> ht();  // Created hash table with capacity C.
        for (int i = 0; i < C; i++) {
          ht.insert(________________, "skittles");
        }
      

   2. Complete the above code so that the total running time is asymptotically proportional to n.
   (In either case, assume that the hash table does not resize.)


6. Consider the following graph:
   
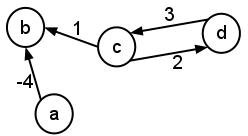
   1. Give the adjacency-list representation of the graph.
   2. Give an adjacency-matrix representation of the graph.


7. (hard) Let G be an undirected graph with an odd number of vertices. Prove that G contains at least one vertex with an even degree.


8. Play Charlie Garrod's Dijkstra Adventure Game by running dag in a terminal window. Be sure to play once or twice with the --random option:

     $ dag --random
   

   (We're sorry for how tedious the game can be -- the graph is big!)


9. Below is a recursive version of depth-first search. Recursive DFS is extremely simple and elegant if the algorithm does not need to track additional information or return any value:

     dfs(G, src):                           // This function initializes the
         isVisited = new dictionary         // dictionary and calls the
         for each vertex v in G:            // recursive helper function.
             isVisited[v] = false
         recursiveDfs(G, src, isVisited)
   
     recursiveDfs(G, src, isVisited):       // This recursive function
         isVisited[src] = true              // searches the graph.
         for each neighbor v of src:
             if !isVisited[v]:
                 recursiveDfs(G, v, isVisited)
     

   1. Execute dfs on the following graph, using s as the source vertex. Draw the stack diagram for the program as it executes. (Assume that isVisited refers to a single copy of the dictionary for all frames of the stack.)
      
   2. Modify the pseudocode above to accept a second vertex, dest, as an argument. Return true if there is a path from src->dest in G, and return false otherwise.
   3. Modify the pseudocode again to return the length of some src->dest path (not necessarily the shortest path) if there is a path from src to dest in G. If there is no src->dest path, return -1.
   4. Write a version of breadth first search and depth first search that determines if a graph is connected.


10. What is the run time of breadth first search? depth first search? Dijkstra's Algorithm? Provide a summary (just a couple sentences) justification for each.

Home Page