Week 7: top-down design (TDD)
Monday
This week and next week we are working on top-down design. This is a useful technique for writing larger, more complex programs. Today (Monday) we will learn about file input and output, so we can use data stored in files in our programs. On Wednesday we will start learning TDD.
Files
Motivations and possible uses:
-
video game data files (read in terrain data; keep track of high scores)
-
grader program: store student grade data in a file (don’t have to type it in each time the program runs)
-
iTunes: how does iTunes keep track of number of plays for each song??
Files can be just text files, like you edit with atom.
syntax
The basic syntax for opening a file is:
myfile = open(filename,mode)
where filename is the name of a file, and mode is the mode used
for opening: usually read ("r") or write ("w") mode. Both arguments are strings,
and myfile is just the variable I picked to store the file object
returned by the open() function.
Here is an example of opening a file called poem.txt for reading,
and storing the file object in a variable called infile:
infile = open("poem.txt", "r")
examples
Once you have a file object, you can use the input and output methods on the object.
OUTPUT
Here’s how to open a file for writing (note: myfile is a variable
name that I choose, and "newfile" is the name of the file to write to):
$ python3
>>> myfile = open("newfile", 'w')
>>> myfile.write("write this to the file \n")
>>> myfile.write("and this.... \n")
>>> myfile.close()
and here are the results of this:
$ ls newfile $ cat newfile write this to the file and this....
What happens if we leave out the \n on each line??
INPUT
I have a file called words.txt with a few words in it:
$ cat words.txt happy computer lemon zebra
To open a file for reading, use 'r' mode:
>>> infile = open("words.txt", 'r')
File words.txt must exist, otherwise we get an error.
The infile variable, which is a FILE type, can be used as a sequence
(e.g., in a for loop!):
>>> for line in infile: ... print line ... happy
computer
lemon
zebra
We can use the for loop like above, or we could use the
file methods: readline() to read one line,
readlines() to read them all at once.
>>>> # need to close and reopen to get back to start of file
>>> infile.close()
>>>
>>> infile = open("words.txt", "r")
>>> word = infile.readline()
>>> print word
happy
>>> word = infile.readline() >>> print word computer
>>> infile.close()
>>> infile = open("words.txt", "r")
>>> words = infile.readlines()
>>> print words
['happy\n', 'computer\n', 'lemon\n', 'zebra\n']
So readlines() reads in EVERYTHING and puts each line into a python list.
NOTE: the newline characters are still part of each line!
Sometimes you want to read in EVERYTHING, all at once.
Sometimes it’s better to read data in line-by-line and process
each line as you go (use the for loop: for line in infile)
File I/O Notes:
-
reading from and writing to files is usually S L O W
-
for this reason, we usually read in data at the beginning of a program and store it in a list or other data structure (ie, if we need the data throughout the program, it’s much faster to refer to the list rather than the file)
-
also, reading from the file is similar to watching a movie on VHS tapes — at the end of the movie, you have to rewind the tape to get back to the beginning. Once we do that
for line in infileloop above, we are at the end of the file. You can "rewind" the file by closing and reopening it (or use theseek()method in python)
str methods: strip() and split()
Suppose we have a file of usernames and grades, like this:
$ cat grades.txt emma: 99 sydney: 87 alex: 95 lauri: 90 jeff: 65 scout: 70 lisa: 88 aline: 78 charlie: 72
If I want to find the average of all of those grades, I need to read
in each line, then somehow pull out the grade and store it. This is
where the str methods strip() and split() can be used. Here are
examples of each:
>>> infile = open("grades.txt", "r")
>>> line = infile.readline()
>>> print(line)
emma: 99
>>> data = line.split(":")
>>> print(data)
['emma', ' 99\n']
>>> grade = float(data[1])
>>> print(grade)
99.0
So split() just splits a string and returns the results as a list.
In the above example we split the string on a colon (":"). Here are a
few more examples of split(). By default (with no arguments given), it
splits the string on whitespace.
>>> S = "a,b,c,d,e,f,g"
>>> L = S.split(",")
>>> print(L)
['a', 'b', 'c', 'd', 'e', 'f', 'g']
>>> phrase = "the quick brown fox jumped over the lazy dog"
>>> words = phrase.split()
>>> print(words)
['the', 'quick', 'brown', 'fox', 'jumped', 'over', 'the', 'lazy', 'dog']
And strip() will strip off leading and trailing characters. Again, by
default it strips off whitespace. If you provide an argument, it will
strip off that:
>>> S = " hello\n"
>>> print(S)
hello
>>> print(S.strip())
hello
>>>
>>> word = "Hello!!!!!"
>>> print(word.strip("!"))
Hello
Your turn
Can you write a program to read the grades.txt file into a python list
of grades, and then calculate the average grade?
Here’s an example of what we want:
$ python3 grader.py [99.0, 87.0, 95.0, 90.0, 65.0, 70.0, 88.0, 78.0, 72.0] average grade: 82.7
challenge
Once you have the grades in a list, can you find the highest and lowest grades?
$ python3 grader.py [99.0, 87.0, 95.0, 90.0, 65.0, 70.0, 88.0, 78.0, 72.0] average grade: 82.7 highest grade: 99.0 lowest grade: 65.0
Wednesday
Here’s the grades.py program from last time:
def main():
grades = readFile("grades.txt")
print(grades)
ave = calcAverage(grades)
print("average grade = %.1f" % (ave))
def calcAverage(grades):
"""given list a grades, calc and return avg grade"""
total = 0
for i in range(len(grades)):
total = total + grades[i]
ave = total/len(grades)
return ave
def readFile(filename):
"""open filename, get grades, return as list"""
inf = open(filename, "r")
lines = inf.readlines()
inf.close()
grades = []
for i in range(len(lines)):
data = lines[i].split(":")
grades.append(float(data[1]))
return grades
main()The readFile() function takes care of opening the file, reading in the
data, converting it to a float, and adding it to a grades list. That
list of grades is then returned to main(), where we can do other stuff
(like calculate the average grade) with the grade data.
top-down design
As we write bigger and more complex programs, designing them first will
save time in the long run. Similar to writing an outline for a paper,
using top-down design means we write out main() first, using functions
we assume will work (and that we will write, later). We also decide on
any data structures we will need.
What we want to avoid is writing a whole bunch of functions and code, and then realizing we forgot something, which changes some of the functions, which changes other functions, and so on.
Furthermore, we want a way to test each function as we write it. Many first-time programmers will write lots of functions and then start testing them. If each function has a few bugs in it, this makes it a lot harder to debug.
A typical top-down design includes the following:
-
main()all written out -
function stubs written (
defwith params, function comment, dummyreturnvalue) -
data structures clearly defined (store data in a list? an object? a list of objects? something else?)
-
the design should run without any syntax errors
-
running the design should show how the program will eventually work
Once you have the design all written out, you can now attack each function one-at-a-time. Get the function to work. Test it to make sure it works, then move on to the next function.
TDD example
Suppose we want to write this square word game:
$ python3 squarewords.py l|l|e d|c|o r|r|a word 1? corralled Correct! Score = 10 g|p|i l|l|a g|i|n word 2? Incorrect...word was: pillaging Score = 0 d|i|n g|a|c c|o|r word 3? according Correct! Score = 10 s|n|i d|a|o o|t|n word 4? quit
The game uses 9-letter words, and displays them in a 3x3 box, where the letters run either vertically or horizontally, and the start of the word can be anywhere in the 3x3 box. The user’s job is to figure out each 9-letter word.
Here’s my TDD for the above program:
"""
squareword puzzle game as example of tdd
J. Knerr
Fall 2019
"""
from random import *
def main():
words = read9("/usr/share/dict/words")
score = 0
done = False
while not done:
word = choice(words)
display(word)
answer = getInput()
if answer == "quit":
done = True
elif answer == word:
score += 10
print("Correct! Score = %d" % (score))
else:
score -= 10
print("Incorrect...word was: %s Score = %d" % (word,score))
def display(word):
"""display word in 3x3 grid with random start position"""
print(word)
def getInput():
"""get user's guess, make sure it's valid, return valid guess"""
guess = input("word? ")
# should allow 9-letter word, quit, and empty string
return guess
def read9(filename):
"""read all 9-letter words from file, shuffle the order, return list"""
words = ["aaaaaaaaa","prototype","ccccccccc"]
return words
main()Notice that main() is completely written! And the goal is that it
shouldn’t need to change much, as I implement the remaining functions.
Also, the program runs, but doesn’t really do much yet (since I haven’t really written all of the functions). Here’s what it looks like so far:
$ python3 design-squarewords.py aaaaaaaaa word 1? 123 Incorrect...word was: aaaaaaaaa Score = -10 prototype word 2? prototype Correct! Score = 0 ccccccccc word 3? quit
Now, since I have a working program (it runs without syntax errors!), I can attack each function separately. I want to write a function and thoroughly test it before I move on to the next function.
Friday
-
did quiz 3
-
worked on lab 6
Second Monday of TDD
Just for fun, we looked at the whole semester, and where we are:
WEEK 1: UNIX/editing/basic python types, functions WEEK 2: for loops, numbers, strings WEEK 3: booleans, if/elif/else branching WEEK 4: while loops, writing simple functions WEEK 5: more complicated functions, stack diagrams WEEK 6: intro to object.method(), graphics WEEK 7: top-down design, writing bigger programs
So we’ve covered most of the python we will learn in this course. The upcoming weeks will look more at algorithms and the analysis of algorithms (e.g., which sorting function is best):
WEEK 8: more top-down design WEEK 9: searching, analysis of algorithms WEEK 10: sorting WEEK 11: recursion (a function that calls itself!) WEEK 12: classes (creating our own objects) WEEK 13: more on classes
The one exception is classes, where we will learn the python syntax of writing our own objects.
start of online classes
There’s a lot of new software we need to install to make this an online class. Please email me or message me on slack if you are having any trouble with the online course (atom, ssh, zoom, slack, understanding the material, etc).
review of top-down design:
Here’s the goal of the TDD process (and what you need to do for lab 7):
-
design the whole program (main and functions) first, before writing all of the code
-
I write out
main(), deciding what functions I will need, and immediately write the function stub -
after doing that, I have a program that runs (no syntax errors), but doesn’t really do much yet, since I haven’t written the full functions
-
now I can do what’s called "bottom-up implementation" and implement each function, one at a time (write it, test it, run it)
review of squarewords program
Here are the requirements for the squarewords game:
-
read in 9-letter words from /usr/share/dict/words
-
allow user to type:
-
9-letter word: to guess the word
-
quit: to quit the game
-
empty string: give up on this word, but keep playing
-
-
keep track of score (+10 if correct, -10 if incorrect)
-
keep track of how many words displayed
And here’s a sample run of the final program:
$ python3 squarewords.py e|r|b e|l|e a|g|u word 1? beleaguer Correct! Score = 10 t|t|l e|m|e n|c|a word 2? cattlemen Correct! Score = 20 a|n|l i|e|r u|n|m word 3? zebra Please enter a 9-letter word! word 3? vegetable Incorrect...word was: unmanlier Score = 10 i|a|e e|n|g v|c|r word 4? (user just hit Enter here) Incorrect...word was: grievance Score = 0 n|s|s c|e|c e|n|o word 5? quit
If you look in jk_squarewords.py, there’s an example of what we want
for lab 7: just the design this week, next week we will implement the
full game.
review reading data from file
Let’s implement the read9(filename) function from the game.
Here’s what we want the function to do:
-
give a file name, open the file for reading
-
read in all words from the file (one per line)
-
only add the 9-letter words to a list, and only those words with alphabetic characters (i.e., no apostrophes or other odd characters)
-
return the list of valid 9-letter words
Here’s the final code for the read9(filename) function:
def read9(filename):
"""read in all 9-letter words, return as list"""
# read in all lines
inf = open(filename, "r") # open file for reading
lines = inf.readlines()
inf.close()
# only add 9-letter, all alphabetic words to the list
words = []
for i in range(len(lines)):
word = lines[i].strip()
if len(word)==9 and word.isalpha():
words.append(word)
# return the valid words list to main
return wordsOnce we’ve written that, we can now run the design again and make sure it works. If it does, we move on to the next function in our game.
Second Wednesday of TDD
The video lecture recorded this time!
But I didn’t think that the chat messages weren’t being recorded. If you are viewing this later, some things I talk about in the video might not make sense. I was answering questions in the chat box. Next time I’ll try to speak the questions before I answer them.
atom tips
As our programs get longer, the more you know about atom, the more
efficient you will be editing your programs. Take a look at the
atom-practice.py file back in your labs/00 directory to improve your atom skills!
list-of-lists review
Sometimes a list-of-lists is the best data structure. For the duo lingo program we are writing today, or any key-value pairs, a list-of-lists is one way to store the data:
>>> LOL = [["A",1],["B",2],["C",3],["D",4]] >>> LOL [['A', 1], ['B', 2], ['C', 3], ['D', 4]] >>> from random import shuffle >>> shuffle(LOL) >>> LOL [['D', 4], ['B', 2], ['A', 1], ['C', 3]] >>> LOL[0] ['D', 4] >>> LOL[0][0] 'D' >>> LOL[0][1] 4
another top-down design
Let’s write a program that mimics part of the duolingo language-learning app.
Here are the requirements for our program:
-
read in english:spanish pairs from file spanish.txt
-
shuffle the pairs, then ask 5 english words/phrases (user types in corresponding spanish words/phrase)
-
if they get the answer correct, let them know
-
if not, show the correct answer
-
if they get 3 in a row correct, print a "good work!" message
-
at the end, if they’ve missed any questions, keep asking the missed questions until they get them all correct
Here’s an example of a few lines from the spanish.txt file:
you are welcome:de nada good morning:buenos dias the apple:la manzana the boy:el nino thanks:gracias
Here’s an example of the running program:
$ python3 duolingo.py i eat bread: yo como pan Correct!! man: hombre Correct!! thanks: gracias Correct!! 3 in a row...good work!! :) woman: nina Nope. woman = mujer i am: yo si Nope. i am = soy woman: mujer <-- one I missed, so it asks again Correct!! i am: you soy <-- another I missed Nope. i am = soy i am: yo soy Nope. i am = soy i am: soy <-- keeps asking until correct Correct!!
Extra features
If you have time: sometimes duo lingo changes the order and shows the spanish, asking for the english. Add this to your program (randomly decide which way to ask):
man: hombre Correct!!
gracias: thanks Correct!!
Second Friday of TDD
Here’s the video recording of today’s lecture:
administrivia
-
Office Hours this afternoon on slack: after class until around 2:30pm
-
Still working on grading (I am behind)…have Q3, L5, L6 to give back hopefully early next week
-
Still waiting on some L7 TDDs — finish your design, run handin21, email tdd at cs.swarthmore.edu telling us you are done with design
-
Today:
-
start of analysis of algorithms (use the rest of the way)
-
write "find largest item in a list" algorithm
-
-
run
update21to getjk_duolingo.pycode from last time
find max of list
Given a list of numbers, can you find the largest number in the list?
[11, 46, 77, 26, 47, 68, 71, 88, 68, 39]
It’s not hard for our brains to solve that problem. Can you write out the steps you used to do that as an algorithm?
In findmaxoflist.py add your findMax(L) function:
def main():
# read in 10.txt or 20.txt, etc
fn = input("filename? ")
data = read(fn)
print(data)
max = findMax(data)
print(max)
# add your findMax(data) function here
def read(filename):
"""read in integers from a file, return as a list"""
# open file, read in all lines
inf = open(filename, "r")
lines = inf.readlines()
inf.close()
# turn lines into list of integers
data = []
for i in range(len(lines)):
line = lines[i]
data.append(int(line))
return data
main()I’ve provided a few files to test your function:
filename answer/max 10.txt 88 20.txt 95 100.txt 965 10000.txt 99986
find index of largest item
Sometimes we want to just find the largest item (as above), but sometimes we want to know where the largest item is in a list. For example, in two weeks we will write functions to sort a list. We might want to find where the largest item is, so we can swap or move it to the front of the list (e.g., if sorting from largest to smallest).
Here’s the findMax(L) code from above:
def findMax(L):
"""given a list, find largest item"""
bsf = L[0] # biggest so far
for i in range(len(L)):
if L[i] > bsf:
# found a larger value,
# so save it to bsf
bsf = L[i]
return bsfHow do we change the above to save and return the index of the largest item?
analysis of algorithms
How does the number of operations in your findMax(L)
function depend on the size of the list? By "operations"
I mean, how many things does the computer have to do?
For example, in the first line of the findMax(L) function (the
bsf=L[0] line) there’s an assignment. Then there’s the for loop,
which loops len(L) times. And in the loop there’s a comparison
operation (if L[i] > bsf). In the if block the assignment will
happen sometimes, and finally there’s the return statement.
If N is the number of items in the list (len(L)), then there are N comparisons
happening in the function, plus a few other operations (a few
assignments). If N is really large (millions or more), then the number
of comparisons dominates, and is a good estimate of the total number of
things happening in this function.
We want to classify algorithms into broad categories. Using how the number of steps or operations varies with the size of the data is one way to classify algorithms.
In the findMax(L) function, if there are 1,000,000 items in the list,
then there are roughly 1,000,000 comparison operations happening.
Similarly, if there are 2,000,000 items, then about 2,000,000
operations.
two algorithms to compare
I’ve got two algorithms to consider, which I am calling the handshake algorithm and the introductions algorithm. Here are short descriptions of each:
-
handshake: suppose I have a class full of 34 students, and I want to meet each of my students. To do this, I walk around and say "Hi, I’m Jeff" to each student and shake their hand.
-
introductions: suppose I now want to introduce each student to every other student in the class. I start by taking the first student around to every other student and introducing them. Then I go back and get the second student, take them to every other student (minus the first one, since they’ve already met), and introduce them, and so on…
When deciding which algorithm to use, programmers are usually interested in three things: run time, memory usage, and storage required (disk space). If your program takes too long to run, or needs more memory than the computer has, or needs more data than can fit on the hard drive, that’s a problem.
For this class, when analyzing algorithms, we will just focus on how many "steps" or operations each algorithm requires. For the handshake algorithm above, it will obviously require 34 handshakes if I have 34 students in my class. However, to classify this algorithm, I would really like to know how the number of handshakes changes as I change the number of students in my class. For example, here’s a simple table showing number of students vs number of handshakes:
| number of students | number of handshakes |
|---|---|
34 |
34 |
68 |
68 |
136 |
136 |
272 |
272 |
Hopefully it is obvious that, if the number of students doubles, the number of handshakes also doubles, and the number of handshakes is directly proportional to the number of students.
linear algorithms: O(N)
The handshake algorithm is an example of a linear algorithm, meaning that the number of steps required, which is ultimately related to the total run time of the algorithm, is directly proportional to the size of the data.
If we have a python list L of students (or student names, or integers,
or whatever), where N=len(L), then, for a linear algorithm, the number
of steps required will be proportional to N.
Computer scientists often write this using "big-O" notation as O(N), and we say the handshake algorithm is an O(N) algorithm (the O stands for "order", as in the "order of a function" — more on this below).
An O(N) algorithm is also called a linear algorithm because if you plot the number of steps versus the size of the data, you’ll get a straight line, like this:
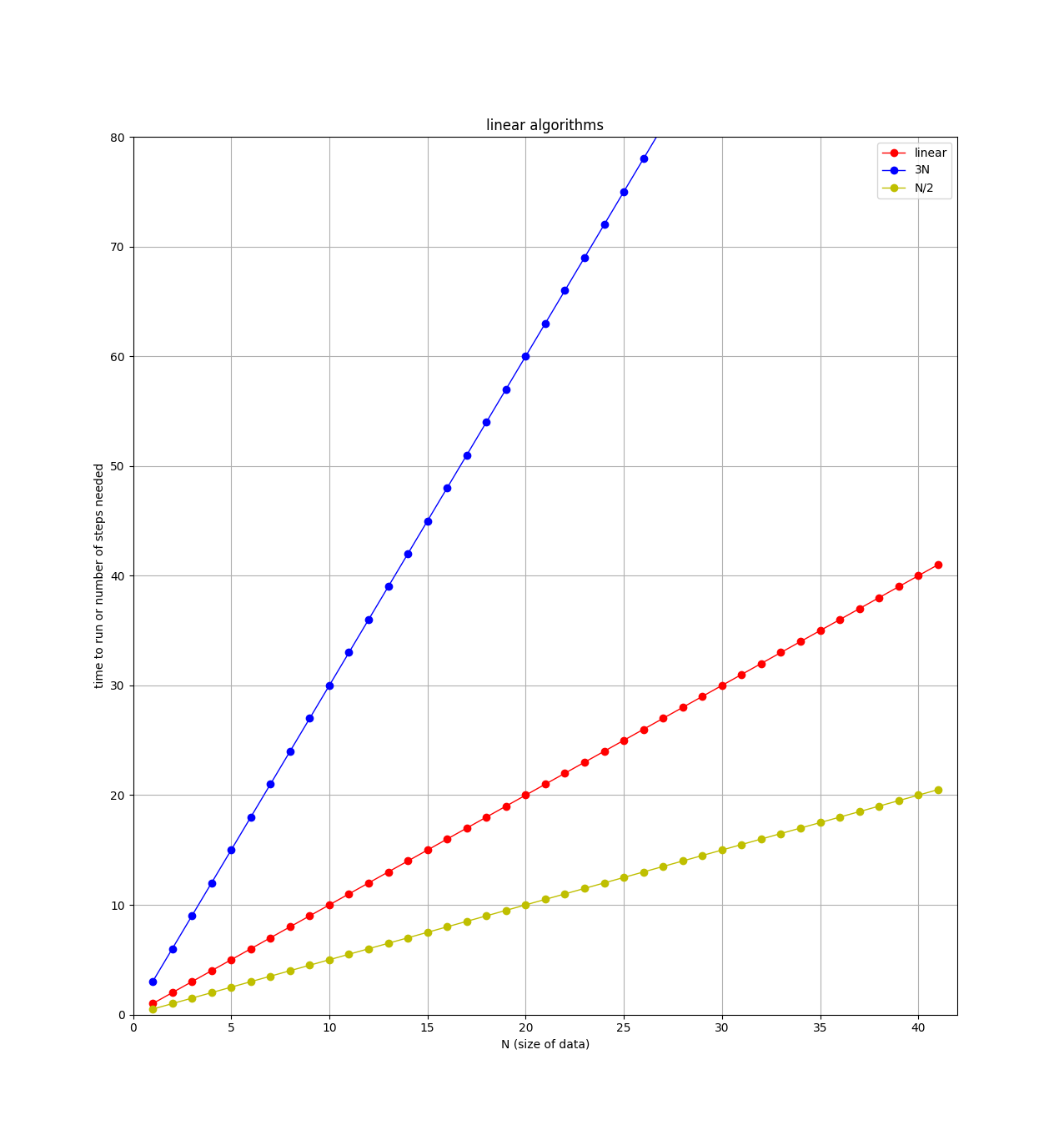
Note on the plot that there are 3 straight lines. When comparing
algorithms, you might have one algorithm that requires N steps, and
another that requires 3*N steps. For example, if I modify the
handshake algorithm to not only shake the student’s hand, but also ask
them where they are from, and write down their email address, then this
algorithm requires 3 steps (shake, ask, write down) for each student. So
for N students, there would be 3*N total steps. Clearly the
algorithm that requires the least steps would be better, but both of
these algorithms are classified as "linear" or O(N). When classifying
algorithms and using the big-O notation, we will ignore any leading constants.
So algorithms with 3*N steps, N steps, N/2 steps, and 100*N
steps are all considered as "linear".
findMax(L) again…
When searching for the largest item in a list, a simple search involves looking at each item in the list to see if it is bigger than all the others you have already seen
def findMax(L):
"""given a list, find largest item"""
bsf = L[0] # biggest so far
for i in range(len(L)):
if L[i] > bsf:
# found a larger value,
# so save it to bsf
bsf = L[i]
return bsfThis is a classic example of a linear algorithm (number of steps directly proportional to the size of the list).
quadratic algorithms: \$O(N^2)\$
For the introduction algorithm discussed above, how many introductions are required? We can count them and look for a pattern. For example, suppose I had only 6 students, then the number of introductions would be:
5 + 4 + 3 + 2 + 1 = 15
Remember, the first student is introduced to all of the others (5 intros), then the second student is introduced to all of the others, minus the first student, since they already met (4 intros), and so on.
If I had 7 students, then the number of introductions would be:
6 + 5 + 4 + 3 + 2 + 1 = 21
and if I had N students:
(N-1) + (N-2) + (N-3) + ... + 3 + 2 + 1 = ???
If you can see the pattern, awesome! Turns out the answer is
\$\frac{(N-1)(N)}{2}\$ introductions for a class of size N.
Try it for the N=6 and N=7 cases:
>>> N=6 >>> (N/2)*(N-1) 15.0 >>> N=7 >>> (N/2)*(N-1) 21.0
Another way to see that is with a bar chart showing how many introductions each student will make:
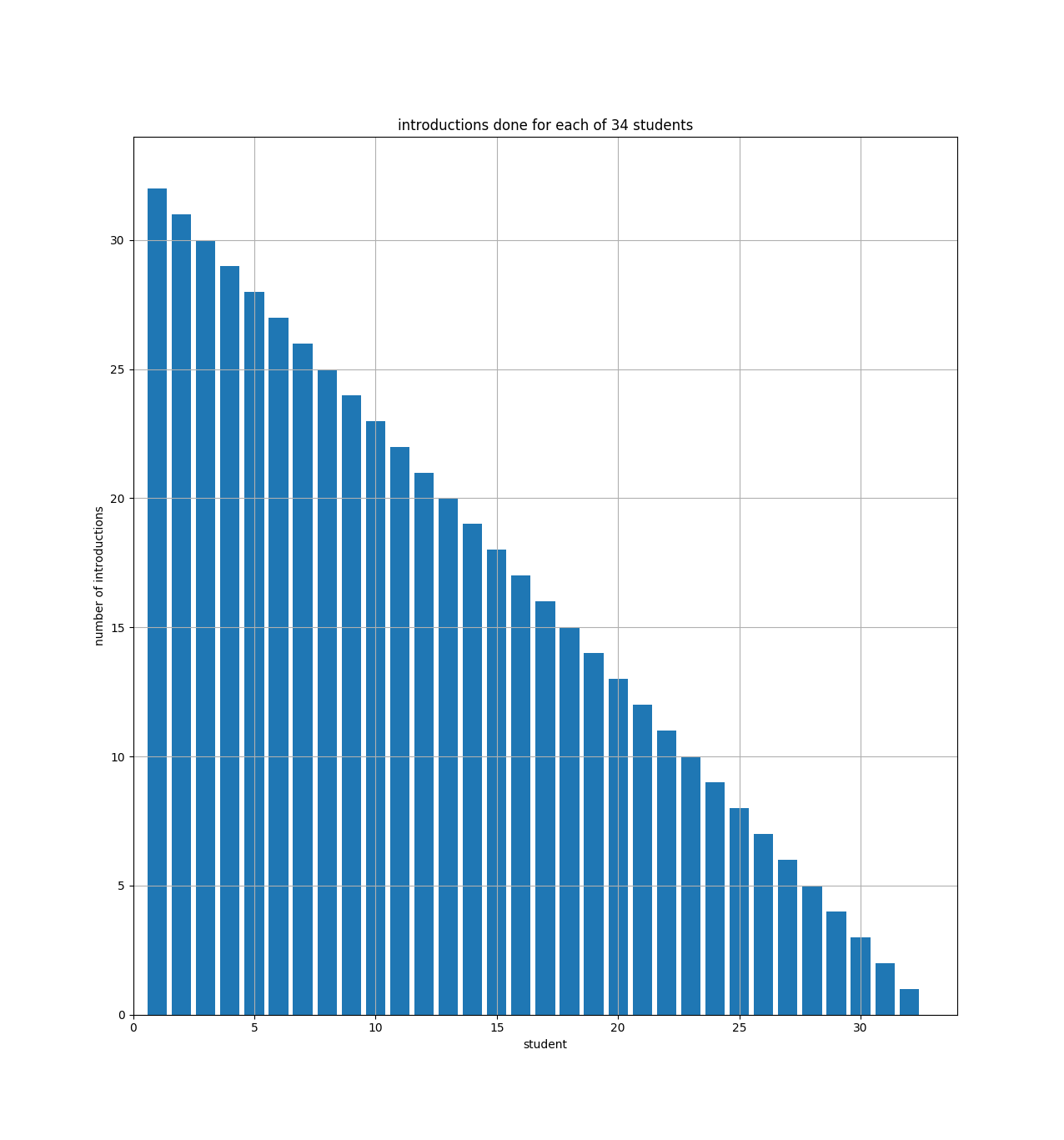
The bar chart just shows that student number 1 (on the x axis) has to do 33 introductions (the y axis), and student number 2 has to do 32, etc. And you can see how the bars fill up half of a 34x34 square. So if we had N students, the bar chart would fill up half of an NxN square.
For the equation above (\$\frac{(N-1)(N)}{2}\$), if you multiply it out, the leading term is N-squared over 2 (i.e., half of an NxN square).
When comparing algorithms, we are mostly concerned with how they will
perform when the size of the data is large. For the introductions
algorithm, the number of steps depends directly on the square of N.
This is written in big-O notation as
\$O(N^2)\$
(order N squared).
These types of algorithms are called quadratic, since the number of
steps will quadruple if the size of the data is doubled.
Here’s a table showing the number of introductions versus the number of students in my class:
| number of students | number of introductions |
|---|---|
34 |
561 |
68 |
2278 |
136 |
9180 |
272 |
36856 |
Notice how the number of introductions goes up very quickly as the size of the class is increased (compare to number of handshakes above).